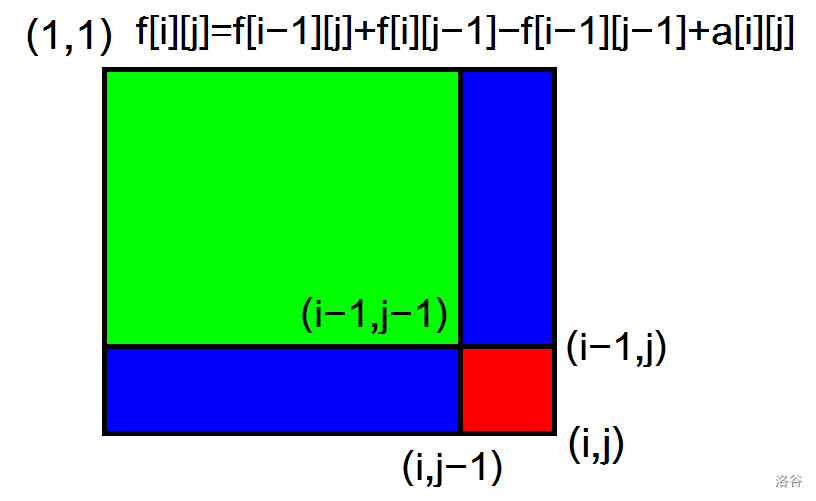反比例函数
最近,有部分同学抱怨:函数好难!怎么都不知道该如何去解……甚至还出现了一个有关函数的诗歌: 晨雾茫茫碍交通,蘑菇核云蔽长空, 化石岁月巧推算,文海索句快如风。 指数对数相辉映,立方平方看对称, 解释大千无限事,三族函数建奇功。 将函数与“晨雾”、“核云”相提并论,可见函数在诸位同学心中的分量之重。其实,那是由于你没有发现函数的“曲线美”。 反比例函数在初中数学的函数学习中,占据着较为重要的位置。下面我们来梳理一下有关反比例函数的知识: 反比例函数的基本内容 定义: 如果两个变量x,y之间的对应关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数。函数表达式为: ◆ y=k/x ◆ y=kxˉ1 ◆ xy=k **注意:**反比例函数成立的条件是:k为常数且k≠0。该条件同时成立,同学在解题过程中往往容易忽视其成立条件,从而在取值范围的确定中易出错。 函数的增减性: 当k>0时,图象分别位于第一、三象限,同一个象限内,y随x的增大而减小; 当k<0时,图象分别位于二、四象限,同一个象限内,y随x的增大而增大。 性质: (1)反比例函数上任何一点与轴 ...
前缀和&线段树&记忆化搜索
<a class="link link--kukuri" data-letters="前缀和">前缀和</a> 1. 一维前缀和 公式: f[i]=∑j=0ia[j]f[i]=\sum_{j=0}^ia[j] f[i]=j=0∑ia[j] 每个计算都要循环一遍,太麻烦了!还有什么办法? 化简:f[i]=a[i]+f[i−1]f[i]=a[i]+f[i-1]f[i]=a[i]+f[i−1] 例题: 给你一个长度为nnn数列,问你mmm个问题,分别是:第b[i]b[i]b[i]个数之前的每一个数相加,和为多少? 先将每一个数算出它的和。 1234for(int i=1;i<=10001;i++){ f[i]=a[i]+f[i-1];//化简公式} 再解决询问的问题。 12345for(int i=1;i<=m;i++){ cin>>b;//输入 cout<<f[b];} 2. 二维前缀和 如图,f[i][j]=f[i−1][j]+f[i][j ...
记忆化搜索
记忆化搜索: 不论是前缀和还是dpdpdp,还是…… 大部分算法都要有动态转移方程。 但是动态转移方程有个缺陷: 有很多动态方程会重复计算好几遍,这会使复杂度大大增加。 但用什么方法来解决此问题呢? 有些人想到了:用一个数组储存函数值。 这就是记忆化搜索。 该算法使用范围:当一个题目根据具体判断可能会出现重复的答案时候,或是不加以优化的暴力搜索会超时的时候,就可以考虑使用记忆化搜索。 e.g.斐波那契数列。 未经过优化的代码: 12345int f(int n){ if(n==1||n==2) return 1; else f(n-1)+f(n-2);} 费时大,许多被重复计算,要算12次。 优化代码: 12345678910long long a[10001];int f(int n){ if(n==1||n==2) return 1; if(a[n]==0) { return a[n]=f(n-1)+f(n-2); } else return a[n];} 用一个数组储存f(n)f(n)f(n)的值,遇到则输出,不然赋 ...
并查集
江湖上散落着各式各样的大侠,有上千个之多。他们没有什么正当职业,整天背着剑在外面走来走去,碰到和自己不是一路人的,就免不了要打一架。但大侠们有一个优点就是讲义气,绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”,只要是能通过朋友关系串联起来的,不管拐了多少个弯,都认为是自己人。这样一来,江湖上就形成了一个一个的帮派,通过两两之间的朋友关系串联起来。而不在同一个帮派的人,无论如何都无法通过朋友关系连起来,于是就可以放心往死了打。但是两个原本互不相识的人,如何判断是否属于一个朋友圈呢? 我们可以在每个朋友圈内推举出一个比较有名望的人,作为该圈子的代表人物。这样,每个圈子就可以这样命名“中国同胞队”美国同胞队”……两人只要互相对一下自己的队长是不是同一个人,就可以确定敌友关系了。 但是还有问题啊,大侠们只知道自己直接的朋友是谁,很多人压根就不认识队长。要判断自己的队长是谁,只能漫无目的的通过朋友的朋友关系问下去:“你是不是队长?你是不是队长?”这样,想打一架得先问个几十年,饿都饿死了,受不了。这样一来,队长面子上也挂不住了,不仅效率太低,还有可能陷入无限循环中。于是队长下令,重新组 ...
三角形的内切圆
一、概念 三角形一定有内切圆,其他的图形不一定有内切圆(一般情况下,n边形无内切圆,但也有例外,如对边之和相等的四边形有内切圆。),且内切圆圆心定在三角形内部。 在三角形中,三个角的角平分线的交点是内切圆的圆心,圆心到三角形各个边的垂线段相等。 内切圆的半径为r=2S/C=S/p,当中S表示三角形的面积,C表示三角形的周长,p表示三角形的半周长。 面积法;1/2lr(l周长)用于任意三角形 二、推论 以内切圆和三角形的三个切点为顶点的三角形A’B’C’是ABC的内接三角形之一。 名称 确定方法 性质 外心(三角形外接圆的圆心) 三角形三边中垂线的交点 到三个顶点的距离相等 外心不一定在三角形内部 内心(三角形内切圆的圆心) 三角形三条角平分线的交点 到三边的距离相等 内心在三角形内部 ABC的内切圆就是A’B’C’的外接圆。而A’A、B’B和C’C三线交于一点,它们的交点就是勒莫恩点(Lemoine point)(或称热尔岗点(Gergonne point)),或类似重心,即三条类似中线的交点。内切圆与九点圆相切,切点称作费尔巴哈点(见九点圆)。 若以三角形的内 ...
唯一分解定理
一、发展简史 算术基本定理是初等数论中一条非常基本和重要的定理,它把对自然数的研究转化为对其最基本的元素——素数的研究。它所体现的唯一因子分解的思想,在现代交换环理论中起着非常重要的作用。唯一因子分解的思想从本质上讲是指以下两种性质: “存在性和唯一性”。所谓“存在性”就是指一个元素可以分解为有限多个不可约因子的乘积;“唯一性”是指这种分解表示在某种意义上来说是唯一的。唯一因子分解的思想最初作为一个自然数的性质而出现,这个性质就是通常所说的算术基本定理。 算术基本定理:任何一个大于 1 的自然数可以分解成一些素数的乘积;并且在不计次序的情况下,这种分解方式是唯一的。算术基本定理起源很早,但将其提炼、明确表述成一条定理,使其在初等数论中获得基础性的地位,却经历了一段较长的时间。 欧几里得(Euclid,约公元前 300 年)是古希腊亚历山大时期著名的数学家,希腊论证几何学的集大成者, 其所著《原本》(在我国通常称为《几何原本》)在数学史、科学史、乃至人类文明史上是一部划时代的杰作,从它问世之日起,备受人们推崇,已用世界各种文字发行了 1000多版,被誉为西方科学的“圣经”。在《原本》中, ...
数学定理大全
数学定理大全 0~9 15定理 6714(黑洞数)定理 A 阿贝尔-鲁菲尼定理 阿蒂亚-辛格指标定理 阿贝尔定理 阿姆达尔定律 阿贝尔二项式定理 艾森斯坦因判别法 奥尔定理 阿基米德中点定理 阿基米德折弦定理 B 波尔查诺-维尔斯特拉斯定理 巴拿赫-塔斯基悖论 伯特兰-切比雪夫定理 贝亚蒂定理 贝叶斯定理 博特周期性定理 闭图像定理 伯恩斯坦定理(康托尔-伯恩斯坦-施罗德定理) 不动点定理 布利安桑定理 布朗定理 贝祖定理 博苏克-乌拉姆定理 半角定理 C 垂径定理 陈氏定理 采样定理 抽屉原理 D 德·摩根定律 迪尼定理 等周定理 代数基本定理 多项式余数定理 大数定律 狄利克雷定理 棣美弗定理 棣莫弗—拉普拉斯定理 笛卡尔定理 多项式定理 笛沙格定理 E 二项式定理 F 富比尼定理 范德瓦尔登定理 费马大定理 法图引理 费马平方和定理 法伊特-汤普森定理 弗罗贝尼乌斯定理 费马小定理 凡·奥贝尔定理 芬斯勒-哈德维格尔定理 反函数定理 费马多边形数定理 G 格林公式 鸽巢原理 高斯—马尔可夫定理 更比定理 谷山-志村定理 哥德尔完备性定理 哥德尔不完备定理 割线定理 广义正交定理 ...