Python 正则表达式一文通
为什么要使用正则表达式 为了回答这个问题,我们先来看看我们面临的各种问题,而这些问题又可以通过使用正则表达式来解决。 考虑以下场景: 文末有一个包含大量数据的日志文件,从这个日志文件中,希望只获取日期和时间。乍一看,日志文件的可读性是很低的。 在这种情况下,可以使用正则表达式来识别模式并轻松提取所需信息。 考虑下一个场景:你是一名销售人员,有很多电子邮件地址,其中很多地址都是假的/无效的,看看下面的图片: 我们可以做的是使用正则表达式,可以验证电子邮件地址的格式并从真实 ID 中过滤掉虚假 ID。 下一个场景与销售员示例的场景非常相似,考虑下图: 我们如何验证电话号码,然后根据原产国对其进行分类? 每个正确的数字都会有一个特定的模式,可以通过使用正则表达式来跟踪和跟踪。 接下来是另一个简单的场景: 我们有一个学生数据库,其中包含姓名、年龄和地址等详细信息。考虑一下地区代码最初是 59006 但现在已更改为 59076 的情况,这种情况为每个学生手动更新此代码将非常耗时且过程非常漫长。 基本上,为了使用正则表达式解决这些问题,我们首先从包含 pin 码的学生数据中找到一个特定的字符 ...
两万字长文让你彻底掌握 celery
这次我们来介绍一下 Python 的一个第三方模块 celery,那么 celery 是什么呢? celery 是一个灵活且可靠的,处理大量消息的分布式系统,可以在多个节点之间处理某个任务; celery 是一个专注于实时处理的任务队列,支持任务调度; celery 是开源的,有很多的使用者; celery 完全基于 Python 语言编写; 所以 celery 本质上就是一个任务调度框架,类似于 Apache 的 airflow,当然 airflow 也是基于 Python 语言编写。 不过有一点需要注意,celery 是用来调度任务的,但它本身并不具备存储任务的功能,而调度任务的时候肯定是要把任务存起来的。因此要使用 celery 的话,还需要搭配一些具备存储、访问功能的工具,比如:消息队列、Redis缓存、数据库等等。官方推荐的是消息队列 RabbitMQ,个人认为有些时候使用 Redis 也是不错的选择,当然我们都会介绍。 那么 celery 都可以在哪些场景中使用呢? 异步任务:一些耗时的操作可以交给celery异步执行,而不用等着程序处理完才知道结果。 ...
Python中的Deque: 实现高效的队列和堆栈
如果经常在 Python 中使用列表,我们会发现,当需要在列表左端弹出和追加元素时,其性能可能不够快。Python 的 collections 模块提供了一个叫做 deque[1] 的类,专门设计用来提供快速和节省内存的方法,以从底层数据结构的两端追加和弹出元素。 Python 中的 deque 是一个低级别的、高度优化的双端队列,对于实现优雅、高效的Pythonic 队列和堆栈很有用,它们是计算中最常见的列表式数据类型。 本文中,云朵君将和大家一起学习如下: 开始使用deque 有效地弹出和追加元素 访问deque中的任意元素 用deque构建高效队列 开始使用Deque 向 Python 列表的右端追加元素和弹出元素的操作,一般非常高效。如果用大 O 表示时间复杂性,那么可以说它们是 O(1)。而当 Python 需要重新分配内存来增加底层列表以接受新的元素时,这些操作就会变慢,时间复杂度可能变成 O(n)。 此外,在 Python 列表的左端追加和弹出元素的操作,也是非常低效的,时间复杂度为O(n)。 由于列表提供了 .append() 和 .pop() 这两种操作,它们可 ...
HarmonyOS 字体
全新 HarmonyOS 字体 通过研究用户在不同场景下对多终端设备的阅读反馈,综合考量不同设备的尺寸、使用场景等因素,同时也考虑用户使用设备时因视距、视角的差异带来的字体大小和字重的不同诉求,我们为 HarmonyOS 设计了全新系统默认的字体——HarmonyOS Sans。 下载 HarmonyOS Sans 全新字体笔画设计 在保障字体体验的功能性前提下,我们在人文和现代中找到新的平衡。在短笔画时保持横平竖直,简约无装饰,撇捺弯钩长笔画中融入书法的笔势美学,带来全新的视觉感受。 优化字体灰度,提升阅读体验 在不同设备的应用场景下,字体的灰度会影响在弱光环境、小字号、远距离下的识别性。因此我们优化字体的灰度,让新字体在不同场景下具有更好的识别性和阅读体验。 统一多语言字形风格 我们重新设计了中文、拉丁文、希利尔文、希腊文、阿拉伯文的字形样式,支持100+语言,让多语言下阅读体验更加一致。 ## HarmonyOS 字体特性 动态字重粗细调节 HarmonyOS Sans支持可变特性,让用户选择他们喜欢的字体粗细来进行文本的显示。 支持更多字重能力 HarmonyOS ...
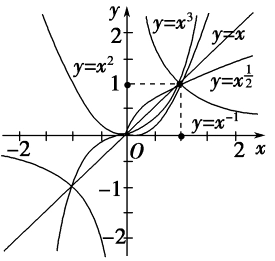
二次函数专题3
二次函数专题3 例题: x2+ax+1>0x^2+ax+1>0x2+ax+1>0在区间[2,3][2,3][2,3]上恒成立,则 aaa 的取值范围是什么? Tips:Tips:Tips: 参变分离 参变分离是求参数取值范围的一种常用方法,通过分离参数用函数观点讨论主要变量的变化情况,由此我们可以确定参数的变化范围,这种方法可以避免分类讨论的麻烦,从而使问题得以顺利解决。参变分离方法在解决不等式恒成立、不等式有解、函数有零点、函数单调性中参数的取值范围等问题中会时常用到。解决这类问题的关键是分离出参数之后将原问题转化为求函数的最值或者值域问题。 不等式两边同除以 xxx 得 x+a+1x>0x+a+\frac {1}{x}>0x+a+x1>0 x+1x>−ax+ \frac{1}{x}>-ax+x1>−a ∵2≤x≤3\because 2≤x≤3∵2≤x≤3 ∴52≤x+1x≤103\therefore \frac {5}{2}≤x+ \frac{1}{x}≤\frac {10}{3}∴25≤x+x1≤310 ∴−a ...
二次函数专题2
二次函数专题2 含参最值讨论问题 课后习题 已知函数f(x)=x2−2ax+4f(x)=x^2-2ax+4f(x)=x2−2ax+4在区间[1,4][1,4][1,4]上的最小值为-8,求参数aaa的值 接下来我们解这一题 f(x)=(x−a)2+4−a2f(x)=(x-a)^2+4-a^2f(x)=(x−a)2+4−a2 当a≤1a≤1a≤1时, f(1)=1−2a+4=5−2af(1)=1-2a+4=5-2af(1)=1−2a+4=5−2a 5−2a=−85-2a=-85−2a=−8 a=132a=\frac {13}{2}a=213 ∵a≤1\because a≤1∵a≤1 ∴舍去\therefore 舍去∴舍去 当1<a<41<a<41<a<4时, f(a)=4−a2f(a)=4-a^2f(a)=4−a2 4−a2=−84-a^2=-84−a2=−8 a2=12a^2=12a2=12 a=23a=2 \sqrt 3a=23 当a≥4a≥4a≥4时, f(4)=16−8a+4=20−8af(4)=16-8a+4=20-8af(4)=16− ...
二次函数专题1
二次函数专题 二次函数 f(x)=ax2+bx+cf(x)=ax^2+bx+cf(x)=ax2+bx+c 根的分布问题 1. x1<x2<kx_1<x_2<kx1<x2<k 通过上图可知 当a>0a>0a>0时, {a>0Δ>0−b2a<kf(k)>0\left\{ \begin{aligned} a>0 \\ \Delta >0 \\ -\frac{b}{2a}<k \\ f(k)>0 \end{aligned} \right.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧a>0Δ>0−2ab<kf(k)>0 当a<0a<0a<0时, {a<0Δ>0−b2a<kf(k)<0\left\{ \begin{aligned} a<0 \\ \Delta >0 \\ -\frac{b}{2a}<k \\ f(k)<0 \end{aligned} \right.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧a<0Δ ...
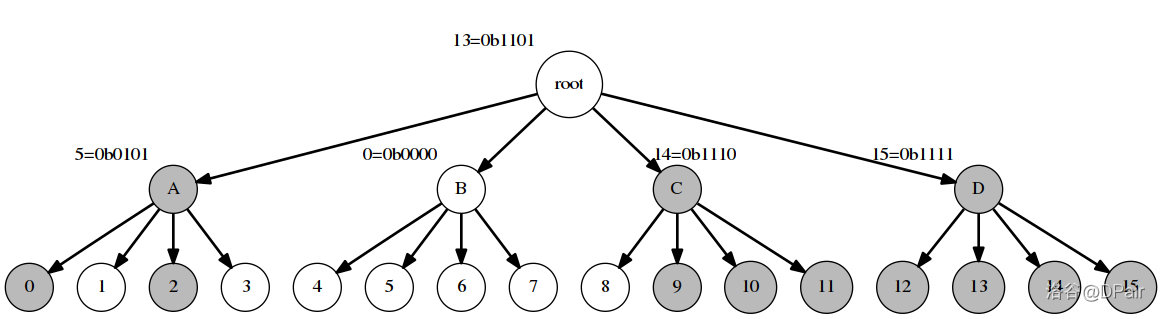
压位 Trie 学习笔记
0 前言 1 Dynamic Predecessor Problem 论文的这一部分主要介绍了 Dynamic Predecessor Problem 是一个怎样的东西,实际上就是 加点删点然后求前驱后继 。论文里另外讲了几种常见的解法,都比较简单在此不赘述。 测试连接 2 压位 trie 2-0 前言 Jacderzhang:“这东西不是很简单吗?去年冬令营wys都讲过。” DPair:“去年冬令营啊,我只记得‘CCF实行三M原则’了……” 2-1 简介 压位 Trie,顾名思义,就是压位的 Trie 树,对于这道题我们显然要对值域开 Trie。 我们发现一般用来处理问题的 Trie 树都是按当前位的 0/10/1 来分类的,最终一次的复杂度是 O(log2V)O(\log_2 V)O(log2V) 的。 这不太行,我们考虑用压位的思想处理这个问题。 那既然你一个结点两个儿子不够,那么我开 w 个儿子,树的深度就降低了,就可以在 O(logwV)O(\log_w V)O(logwV) 的时间内处理问题了。 借用一张论文里面的图,应该可以帮助理解。 上图事实上维护了一个值域为 ...
ETT(Euler Tour Tree)学习笔记
-1. 导入 当维护一个动态变化的树时,最常用的数据结构就是 Link-Cut Tree 了,但是有的毒瘤出题人总是出一些这样的阴间问题: 把以 x 连带它的子树整个接在节点 y 的下面。 把以 x 为根的子树权值都加上 y 。 常规的LCT无法解决这样的问题,怎么办? 肯定有大佬会跳出来说:我会LCT维护虚子树信息! 然而这样简单的LCT就会细节巨多,稍微写错一点就会全部木大。我们需要一种更加适合我这种蒟蒻、更简单的数据结构—— ETT 。 Notice :真正的ETT能够实现更加复杂的功能,然而写起来也更加困难,写题时经常使用的是使用牺牲了一部分功能的简化版,即伪ETT。本文主要介绍的也是伪 ETT 。 0. 目录 什么是 ETT ? ETT 怎么写 ? 2.1. 前置芝士 : 括号序。 2.2. 前置芝士 : 伸展树。 2.3. 操作 1. 把以 x 连带它的子树整个接在节点 y 的下面。 2.4. 操作 2. 查询从 x 到根的和。 2.5. 操作 3. 连接/断开一条从 x 到 y 的路径。 2.6. 操作 4. 给一个以 x 为根的子树内所以节点权值集体加 k ...
有限微积分与数列求和
前言 本文参考自《具体数学》。 如有错漏敬请读者一一指出或喷作者。 可能的前置知识: 组合数及其处理技巧。 两类斯特林数。 拉格朗日插值。 当然不知道也没关系,与这些相关的大多是证明方面的东西。 问题引入 对于数列求和,我们有以下耳熟能详的公式: 1+2+3+⋯+n=∑k=1nk=n(n+1)21+2+3+\cdots+n=\sum_{k=1}^nk=\dfrac{n (n+1) } {2}1+2+3+⋯+n=∑k=1nk=2n(n+1) 1+a+a2+⋯+an−1=∑k=0n−1ak=an−1a−11+a+a^2+\cdots+a^{n-1}=\sum_{k=0}^{n-1}a^k=\dfrac{a^n-1} {a-1}1+a+a2+⋯+an−1=∑k=0n−1ak=a−1an−1 但这些公式缺乏一般性,例如将等差数列求和公式的 kkk 变为 k2k^2k2 或 k3k^3k3: 12+22+⋯+n2=∑k=1nk2=n(n+1)(2n+1)61^2+2^2+\cdots+n^2=\sum_{k=1}^nk^2=\dfrac{n(n+1) (2n+1) } {6}12+22+ ...