幂

AI-摘要
PFS GPT
AI初始化中...
介绍自己
生成本文简介
推荐相关文章
前往主页
前往tianli博客
一、相关介绍
幂(power)是指乘方运算的结果。指该式意义为m个n相乘。把看作乘方的结果,叫做n的m次幂,也叫n的m次方。
数学中的“幂”,是“幂”这个字面意思的引申,“幂”原指盖东西布巾,数学中“幂”是乘方的结果,而乘方的表示是通过在一个数字上加上标的形式来实现的,故这就像在一个数上“盖上了一头巾”,在现实中盖头巾又有升级的意思,所以把乘方叫做幂正好契合了数学中指数级数快速增长含义,形式上也很契合,所以叫做幂。
幂不符合结合律和交换律。
因为十的次方很易计算,只需在后加零即可,所以科学记数法借助此简化记录数的方式;二的次方在计算机科学中很有用。
二、定义
幂指乘方运算的结果。指个相乘。把看作乘方的结果,叫做的次幂。
其中,称为底数,称为指数(写成上标)。当不能用上标时,例如在编程语言或电子邮件中,通常写成或,亦可以用高德纳箭号表示法,写成,读作“的次方”或者的次幂。
当指数为时,通常不写出来,因为那和底的数值一样;指数为时,可以读作“的平方”、“的立方”。
幂的指数是负数时,等于
分数为指数的幂定义为。
证:
令 () 开次方 =
两边取次方,有
开次方
即开次方
幂不符合结合律和交换律。
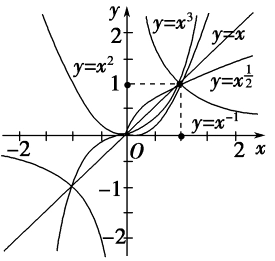
三、大小比较法
计算比较法
先通过幂的计算,然后根据结果的大小,来进行比较的。
底数比较法
在指数相同的情况下,通过比较底数的大小,来确定两个幂的大小。
指数比较法
在底数相同的情况下,通过比较指数的大小,来确定两个幂的大小。
求差比较法
将两个幂相减,根据其差与0的比较情况,来确定两个幂的大小。
求商比较法
将两个幂相除,然后通过商与1的大小关系,比较两个幂的大小。
乘方比较法
将两个幂乘方后化为同指数幂,通过进行比较结果,来确定两个幂的大小。
定值比较法
通过选一个与两个幂中一个幂相接近的幂作定值,然后用两个幂与所选取的定值相比较,由此来确定两个幂的大小。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Panjoel's Blog!
评论
匿名评论
你无需删除空行,直接评论以获取最佳展示效果