0 前言

1 Dynamic Predecessor Problem

论文的这一部分主要介绍了 Dynamic Predecessor Problem 是一个怎样的东西，实际上就是 加点删点然后求前驱后继 。论文里另外讲了几种常见的解法，都比较简单在此不赘述。

测试连接

2 压位 trie

2-0 前言

Jacderzhang：“这东西不是很简单吗？去年冬令营wys都讲过。”

DPair：“去年冬令营啊，我只记得‘CCF实行三M原则’了……”

2-1 简介

压位 Trie，顾名思义，就是压位的 Trie 树，对于这道题我们显然要对值域开 Trie。

我们发现一般用来处理问题的 Trie 树都是按当前位的 0/10/1 来分类的，最终一次的复杂度是 O(log⁡2V)O(\log_2 V) 的。

这不太行，我们考虑用压位的思想处理这个问题。

那既然你一个结点两个儿子不够，那么我开 w 个儿子，树的深度就降低了，就可以在 O(log⁡wV)O(\log_w V) 的时间内处理问题了。

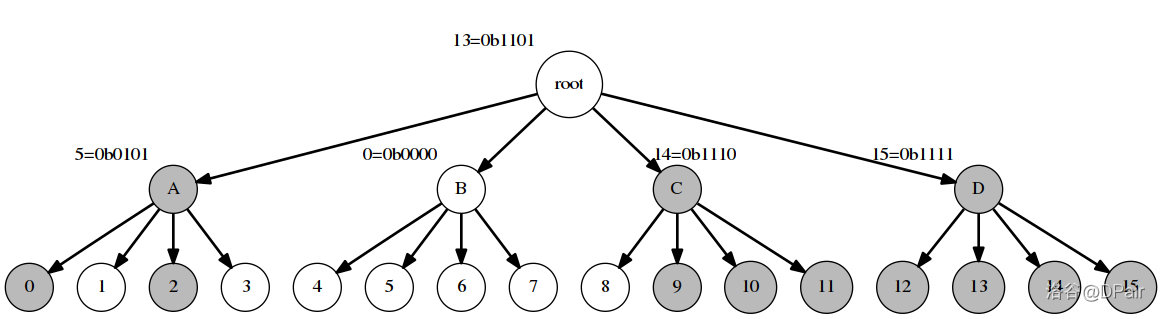
借用一张论文里面的图，应该可以帮助理解。

上图事实上维护了一个值域为 [0,24)[0, 2^4) 的问题，取 w=4 ，所以总层数为 log⁡424=2\log_42^4=2 。每一个结点维护的是自己的子树中 有哪几个有值 。例如图中维护的数字集合就是 {0,2,9,10,11,12,13,14,15}\{0, 2, 9, 10, 11, 12, 13, 14, 15\} ，所有有数的点为深色。

至于为什么 ￥gg 的论文里面 root 没有标深色，我也不知道，但按我个人的理解是要标的。可能是没必要标（毕竟你这个数集里面有没有元素全局维护即可）。

并且，这里我们也可以初步看出，对于一个压位 Trie ，我们一方面不能动态开点（不然要记录儿子）。

2-2 操作处理

回归正题，不难发现我们可以把这棵树看做一棵 leafytree ，当然也可以理解成线段树。这对我们处理修改和询问有一定的帮助。

注：接下来我们认为值域是 2k2^k
即卡满，至于为什么这么写。。。这是因为 DPair 写挂了一个地方然后不想改了（（

upd：好像确实得补到 2k2^k ?

2-2-1 插入

首先我们考虑插入操作，不难发现我们和普通 Trie 的插入方式一致是可以做到的。考虑从根节点开始，往我们插入的方向一直走，沿途打标记即可。复杂度 O(log⁡w2k)O(\log_w 2^k) 。

2-2-2 删除

与插入同理，最后把空的子树标记清除一下即可，同样也是沿途修改。复杂度 O(log⁡w2k)O(\log_w 2^k) 。

2-2-3 前驱后继

这两个没有本质区别，故并举，下面只讨论前驱。

首先我们显然要从根开始往下搜，那么对于在一可子树内找 x 的前驱，我们分两类处理：

这一位就已经 < x ，那么直接在左边最大的子树中查找最大值即可，显然最优。复杂度 O(log⁡w2k)O(\log_w 2^k) 。
这一位 =x ，这一部分需要考虑 x 在自己所对应的子树内有没有前驱，如果有的话显然更优。
所以我们先搜索 2 情况，不合法再搜 1 情况。

咋看之下这东西是 O(log⁡w22k)O(\log_w^22^k) 的。

事实上，不难发现我们可以 O(1)O(1) 判断 1 情况是否有解，故 1 情况最多被执行一次，最终复杂度还是 O(log⁡w2k)O(\log_w2^k) 的。

用 unsigned long long 压位可以压到 w=64 。

2-3 关于空间复杂度

假设树的大小为 2k2^k 。由于不能动态开点，朴素实现的话空间和线段树类似是 O(2k)O(2^k) ，但这对于像我一样的毒瘤出题人们来说过于 naive。不过其实也不难发现这东西的空间优化方式和线段树类似，压位 Trie 的最后一层有 2k2^k 个结点，但本质上什么都没有记录，所以可以直接优化掉，最终为 O(2kw)O({2^k\over w}) 。

2-4 一些优化

￥gg 论文里面说这部分是压位 Trie 的实现，单个人觉得像是在写优化，所以直接当优化去理解了。

首先我们采取分层维护的方式，每一层开一个对应大小的数组来进行维护，可以尽可能压缩空间。

2-4-1 插入

然后不难发现，每一个值在每一层对应的位置都可以非常方便地求出，故插入时考虑自下而上遍历。如果已经插入过的话就可以直接弹出，达到剪枝的效果。

2-4-2 删除

删除同理，如果某一个结点删完之后还有数，那么就可以不继续向上走而直接跳出了。

而且不难发现如果自上而下的话，删除需要上下行两趟操作，现在只需要一趟。

2-4-3 前驱后继

我们还是只讨论前驱。

不难发现，我们自下而上的话，就是从当前的 xx 开始，如果其左侧存在结点，那么就可以直接对应找最大值了，也减少了常数。

这些剪枝已经足够了，而且实现上并不困难。

2-5 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
#include <cstdio>

namespace BITWISE{
    inline int clz(unsigned long long x){return __builtin_clzll(x);}//这个函数是查询开头几个零
    inline int ctz(unsigned long long x){return __builtin_ctzll(x);}//这个函数是查询末尾几个零
} // namespace BITWISE
using namespace BITWISE;
namespace GenHelper{
    unsigned z3, z4, b;
    inline unsigned rand_(){
        z3 = ((z3 & 4294967280U) << 7) ^ ((z3 << 13) ^ z3) >> 21;
        z4 = ((z4 & 4294967168U) << 13) ^ ((z4 << 3) ^ z4) >> 12;
        return (z3 ^ z4);
    }
}
inline void srand_(unsigned x){
    using namespace GenHelper;
    z3 = x ^ 0x1234598766U;
    z4 = (~x) + 51;
}

typedef unsigned long long ull;
const int g = 6;
const int mod = (1 << g) - 1;
ull BUFF[1 << 25], *BT = BUFF + sizeof(BUFF) / sizeof(ull);//预先开好内存池
inline ull *alloc(int sz){return BT -= sz;}//动态分配空间
struct Trie{
    int dep;ull *a[5];//动态数组
    Trie(int sz){//初始化
        dep = 1;
        for(;;++ dep){
            int cnt = (sz + (1ull << g * dep) - 1) >> g * dep;//表示这一层有多少个点
            a[dep - 1] = alloc(cnt);
            if(cnt == 1) return ;
        }
        //注意这里层数越小越深，这样方便我们位运算
    }
    inline void ins(int x){
        for (int i = 0;i < dep;++ i){//自下而上遍历的
            ull p = 1ull << (x >> i * g & mod); //判断我们这个 x 在当前这一层要走哪一条边，并且直接左移好方便压位的处理
            if(a[i][x >> (i + 1) * g] & p) return ;//剪枝，上面有就可以弹出了
            a[i][x >> (i + 1) * g] |= p;
        }
    }
    inline void del(int x){
        for (int i = 0;i < dep;++ i)
            if(a[i][x >> (i + 1) * g] &= ~(1ull << (x >> i * g & mod))) return ;//删除一个位置，同样是删完还有就不删了的剪枝
    }
    inline int succ(int x){
        for (int i = 0;i < dep;++ i){
            int cur = (x >> i * g) & mod;ull v = a[i][x >> (i + 1) * g];//当前是哪一条边，由于这里只需要知道是哪一条边所以我们不需要左移
            if(v >> cur > 1){//如果存在前驱，也可以写成 v >> (cur + 1)，后者更好理解但前者似乎更快
                int res = x >> (i + 1) * g << (i + 1) * g;
                res += (ctz(v >> (cur + 1)) + cur + 1) << i * g;//先把这一层的贡献加上，注意是不完整的
                for (int j = i - 1;~j;-- j) res += ctz(a[j][res >> (j + 1) * g]) << j * g;//剩下每一层都是完整的
                return res;//直接返回
            }
        }
        return 0;//否则返回零
    }
    inline int pre(int x){//与上面同理，不赘述
        for (int i = 0;i < dep;++ i){
            int cur = (x >> i * g) & mod;ull v = a[i][x >> (i + 1) * g];
            if(v & ((1ull << cur) - 1)){
                int res = x >> (i + 1) * g << (i + 1) * g;
                res += (mod - clz(v & ((1ull << cur) - 1))) << i * g;
                for (int j = i - 1;~j;-- j) res += (mod - clz(a[j][res >> (j + 1) * g])) << j * g;
                return res;
            }
        }
        return 0;
    }

};

int ans;
Trie s(1 << 30);
inline void work(){
    int x = GenHelper :: rand_() & ((1 << 30) - 1), op = (x >> 15) & 3;
    /* Your code begins here */
    if(op == 0) s.ins(x);
    else if(op == 1) s.del(x);
    else if(op == 2) ans ^= s.pre(x);
    else ans ^= s.succ(x);
}
int n, seed;
int main(){
    scanf("%d%d", &n, &seed);
    srand_(seed);
    while(n --) work();
    printf("%d\n", ans);
}

3 个人总结

这个数据结构似乎都基于值域，而且似乎使用起来有比较大的限制，所以感觉在我目前能够涉及到的 OI 范围中不太能用上，比如论文里面给出的 [ZJOI2019] 语言 这一例子，我们完全可以使用线段树合并来进行直接处理，代码难度更低的同时同样可以通过这道题。故个人感觉除了卡常需要，这个数据结构一般不太会用上。不过这个思想还是很值得学习的。