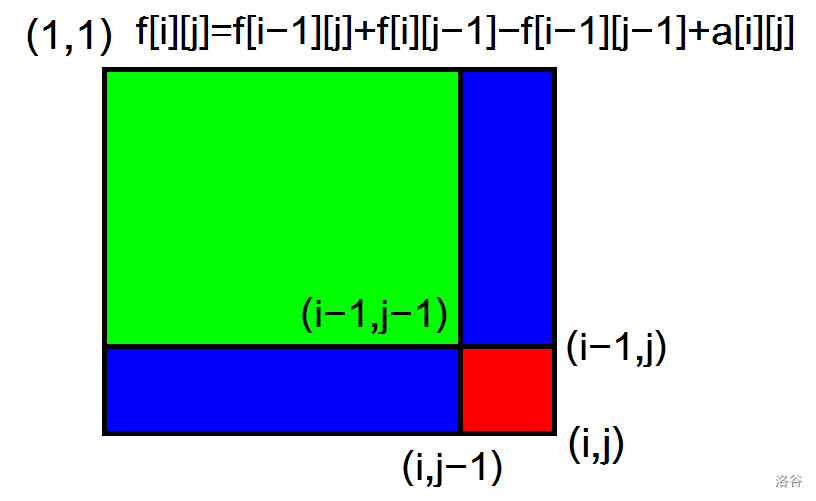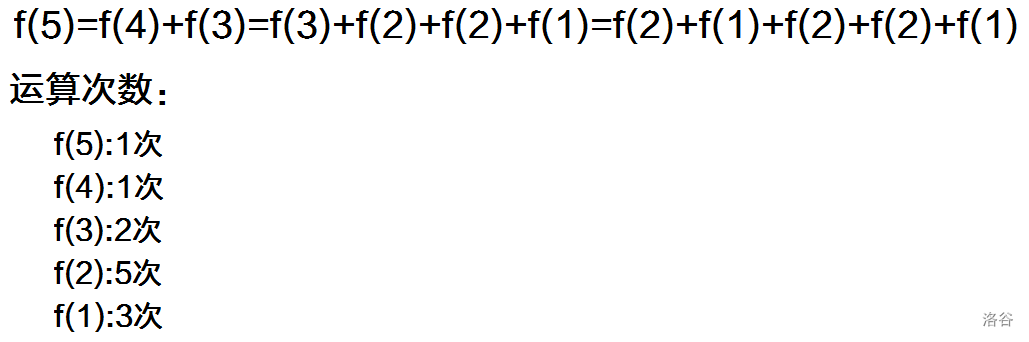<a class="link link--kukuri" data-letters="前缀和">前缀和</a>
1. 一维前缀和
公式:
f[i]=j=0∑ia[j]

每个计算都要循环一遍,太麻烦了!还有什么办法?
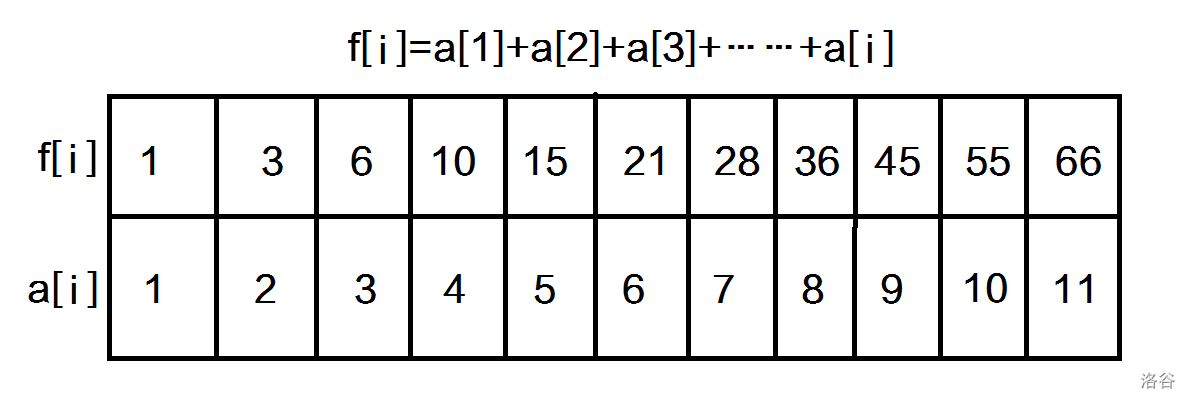
化简:f[i]=a[i]+f[i−1]
例题:
给你一个长度为n数列,问你m个问题,分别是:第b[i]个数之前的每一个数相加,和为多少?
先将每一个数算出它的和。
1
2
3
4
| for(int i=1;i<=10001;i++)
{
f[i]=a[i]+f[i-1];
}
|
再解决询问的问题。
1
2
3
4
5
| for(int i=1;i<=m;i++)
{
cin>>b;
cout<<f[b];
}
|
2. 二维前缀和

如图,f[i][j]=f[i−1][j]+f[i][j−1],但是我们多算了绿块f[i−1][j−1],还少算了红块f[i][j],只要减掉,再加上,就可以啦 。
<a class="link link--kukuri" data-letters="线段树">线段树</a>
1.区间加
输入n,m,分别表示有n个数,m个步骤。
下面1个数x,表示原高度,然后m+2行操作。
操作1:给出L,R,y ,表示在[L,R]区间内,每个数加上y。
操作2:给出L,R,表示询问在[L,R]区间内每个高度之和。
操作1表示为1 L R x。
操作2表示为2 L R。

方案一:将[L,R]区间内,每个数循环加上y。但是复杂度太高。
方案二:将a[L]=x+y,a[R+1]−=y。
然后再用循环a[i]=a[i−1]。
这样复杂度就大大减少啦。
2.区间乘
代码如下,方法与区间加similar:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void cheng(long long l,long long r,long long id,long long tl,long long tr,long long x)
{
if(tl<=l&&r<=tr)
{
ch[id]=((long long)ch[id]*x)%P;
dx[id]=((long long)dx[id]*x)%P;
sum[id]=((long long)sum[id]*x)%P;
return;
}
int mid=(l+r)/2;
if((ch[id]!=1) || dx[id])
{
dx[id<<1]=((long long)dx[id<<1]*ch[id]+dx[id])%P;
ch[id<<1]=((long long)ch[id<<1]*ch[id])%P;
sum[id<<1]=(((long long)sum[id<<1]*ch[id])%P+(LL)dx[id]*(mid-l+1)%P)%P;
ch[id<<1|1]=((long long)ch[id<<1|1]*ch[id])%P;dx[id<<1|1]=((LL)dx[id<<1|1]*ch[id]+dx[id])%P;
sum[id<<1|1]=(((long long)sum[id<<1|1]*ch[id])%P+(LL)dx[id]*(r-mid)%P)%P;
ch[id]=1;dx[id]=0;
}
if(tl<=mid) cheng(l,mid,id*2,tl,tr,x);
if(tr>=mid+1) cheng(mid+1,r,id*2+1,tl,tr,x);
sum[id]=(sum[id<<1]+sum[id<<1|1])%P;
return;
}
|
<a class="link link--kukuri" data-letters="记忆化搜索">记忆化搜索</a>
不论是前缀和还是dp,还是……
大部分算法都要有动态转移方程。
但是动态转移方程有个缺陷:
有很多动态方程会重复计算好几遍,这会使复杂度大大增加。
但用什么方法来解决此问题呢?
有些人想到了:用一个数组储存函数值。
这就是记忆化搜索。
该算法使用范围:当一个题目根据具体判断可能会出现重复的答案时候,或是不加以优化的暴力搜索会超时的时候,就可以考虑使用记忆化搜索。
e.g.斐波那契数列。
未经过优化的代码:
1
2
3
4
5
| int f(int n)
{
if(n==1||n==2) return 1;
else f(n-1)+f(n-2);
}
|

费时大,许多被重复计算,要算12次。
优化代码:
1
2
3
4
5
6
7
8
9
10
| long long a[10001];
int f(int n)
{
if(n==1||n==2) return 1;
if(a[n]==0)
{
return a[n]=f(n-1)+f(n-2);
}
else return a[n];
}
|
用一个数组储存f(n)的值,遇到则输出,不然赋值,只需5次,复杂度O(n)。
可以看出用了记忆化搜索,TLE不用愁!
<a class="link link--kukuri" data-letters="应用">应用</a>
1.前缀和
P1147 连续自然数和
P1387 最大正方形
P1437 [HNOI2004]敲砖块
2.线段树
U121358 在火星上
P1880 [NOI1995]石子合并
P1437 [P4170 [CQOI2007]涂色
3.记忆化搜索
P1464 Function
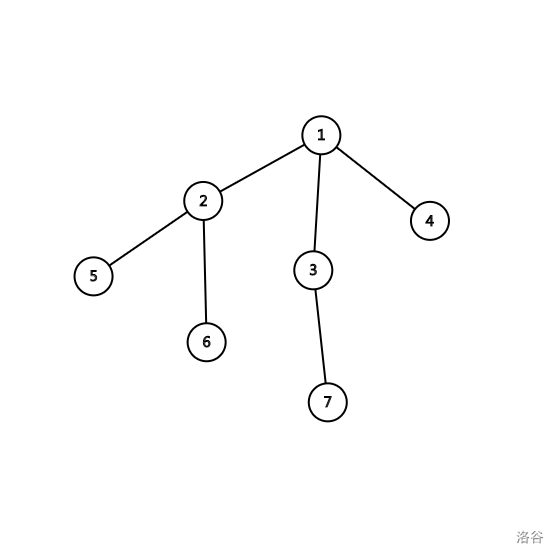
P1352 没有上司的舞会
U121357 找回病人