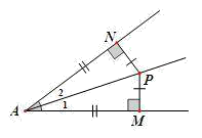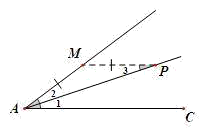一、定义

把一个角平分的射线叫该角的角平分线。

二、性质

  1. 角平分线上的点到角的两边的距离相等。

  2. 角平分线可以得到两个相等的角。

  3. 三角形的三条角平分线交于一点，称作三角形内心。三角形的内心到三角形三边的距离相等。

三、定理

  1. 在角的平分线上的点到这个角的两边的距离相等。

  2. 三角形一个角平分线，这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例，AB:AC=BD:BC。

  3. 在圆中，弧相等，弦相等。

  4. 双平线，若∠1=∠2且BC∥BD，则BC=BD。

四、辅助线

  1. 如下图，由角的平分线上的一点向角的一边或两边作垂线，可以用角的平分线性质定理解题；

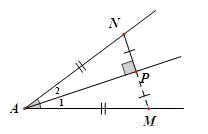
  1. 如下图，以角的平分线为轴，将图形翻折，在角的平分线两侧构造全等三角形，使已知与结论发生关系出现新的条件；

  1. 如下图，当题设有角平分线及与角平分线垂直的线段，可延长这条线段与角的另一边相交，构成等腰三角形，利用等腰三角形的“三线合一” 性质证题；

  1. 如下图，过角的一边上的点，作另一边的平行线，构成等腰三角形——“角平分线+平行，必出等腰 ”.

  1. 如下图，在圆中的角平分线，等弧等弦，辅助线画缺的弧或弦。