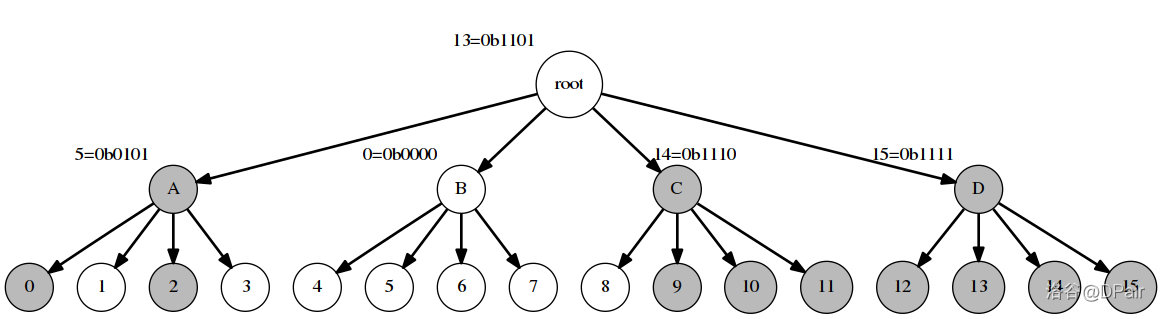
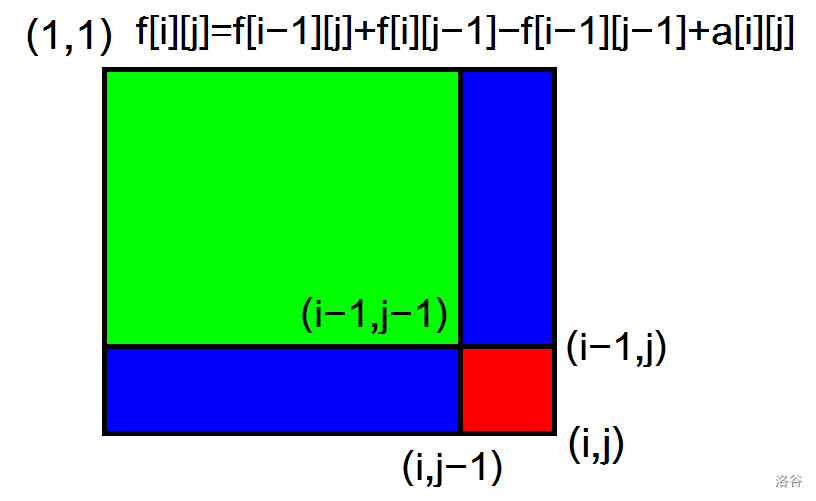一、ST表 1.预处理 f [ i ] [ j ] f[i][j] f [ i ] [ j ] ( ( ( [ i , i + 2 j − 1 ] ) [i,i+2j−1]) [ i , i + 2 j − 1 ] )
递推公式( j (j ( j ): ): ) :
f [ i ] [ j ] = m a x f [ i ] [ j − 1 ] , f [ i + 2 j − 1 ] [ j − 1 ] f[i][j]=max{f[i][j−1],f[i+2j−1][j−1]} f [ i ] [ j ] = m a x f [ i ] [ j − 1 ] , f [ i + 2 j − 1 ] [ j − 1 ]
即将区间[ l , r ] [l,r] [ l , r ]
2.查询 分为两段,第一段为区间[ l , 2 k ] [l,2k] [ l , 2 k ] [ r − 2 k + 1 , r ] [r−2k+1,r] [ r − 2 k + 1 , r ] k k k 2 k ≤ r − l + 1 2k≤r−l+1 2 k ≤ r − l + 1
即区间[ l , r ] [l,r] [ l , r ] m a x f [ l ] [ k ] , f [ r − 2 k + 1 ] [ k ] max{f[l][k],f[r−2k+1][k]} m a x f [ l ] [ k ] , f [ r − 2 k + 1 ] [ k ]
3.例子 忠诚 洛谷 P1816
多次查询区间最小值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <cstdio> #include <algorithm> #include <cstring> using namespace std;int m,n;#define MAXN 100001 #define LOG 18 int st[MAXN][LOG];int lg2[MAXN];int main () scanf ("%d %d" , &n, &m); memset (st, 0x3f , sizeof st); for (int i=1 ;i<=n;++i) scanf ("%d" , &st[i][0 ]); for (int len=1 ;len<LOG;++len) for (int i=1 ;i+(1 <<len)-1 <=n;++i) st[i][len]=min (st[i][len-1 ], st[i+(1 <<(len-1 ))][len-1 ]); for (int i=2 ;i<=n;++i) lg2[i]=lg2[i>>1 ]+1 ; while (m--){ int l,r;scanf ("%d %d" , &l, &r); int sz=lg2[r-l+1 ]; printf ("%d " , min (st[l][sz], st[r+1 -(1 <<sz)][sz])); } return 0 ; }
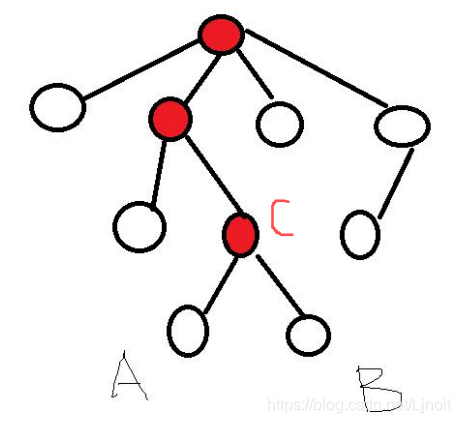
二、树上倍增 1.求解LCA (1) 预处理 首先结合dfs预处理出f [ i ] [ j ] , f [ i ] [ j ] f[i][j],f[i][j] f [ i ] [ j ] , f [ i ] [ j ]
递推公式:
f [ i ] [ j ] = f [ f [ i ] [ j − 1 ] ] [ j − 1 ] f[i][j]=f[f[i][j−1]][j−1] f [ i ] [ j ] = f [ f [ i ] [ j − 1 ] ] [ j − 1 ]
即节点i分两次向上跳,每次跳2 j − 1 2^{j−1} 2 j − 1 i i i 2 j 2^j 2 j ( 2 j − 1 × 2 = 2 j ) (2^{j−1}×2=2^j) ( 2 j − 1 × 2 = 2 j )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void load (int x, int fa) f[x][0 ]=fa; dep[x]=dep[fa]+1 ; for (int i=1 ;i<20 ;++i) f[x][i]=f[f[x][i-1 ]][i-1 ]; } void dfs (int u, int fa) load (u, fa); for (int i=head[u];i;i=nxt[i]){ int v=vv[i]; if (v==fa) continue ; dfs (v, u); } }
同时也可以像下面预处理出l o g 2 n log^n_2 l o g 2 n
1 2 for (int i=2 ;i<=tot;++i) lg2[i]=lg2[i>>1 ]+1 ;
(2) 查询 首先使两个查询节点跳至同一高度后(因为它们的最近公共祖先不可能低于这两点,跳跃方法同下),当前层记为x x x l o g 2 x log^x_2 l o g 2 x 0 0 0 j j j 2 j 2^j 2 j 2 0 2^0 2 0 i i i f [ i ] [ 0 ] f[i][0] f [ i ] [ 0 ]
其中,可以直接从最大可能的i i i i i i
1 2 3 4 5 6 7 8 9 10 11 inline int lca (int a, int b) if (dep[a]<dep[b]) swap (a, b); for (int i=20 ;i>=0 ;--i) if (dep[f[a][i]]>=dep[b]) a=f[a][i]; if (a==b) return a; for (int i=20 ;i>=0 ;--i) if (f[a][i]!=f[b][i]) a=f[a][i], b=f[b][i]; return f[a][0 ]; }
这是一种在线求LCA的算法,其实还有Tarjan这种效率高的离线算法。
2.O ( 1 ) O(1) O ( 1 ) 另外还有一种n l o g n nlogn n l o g n O ( 1 ) O(1) O ( 1 )
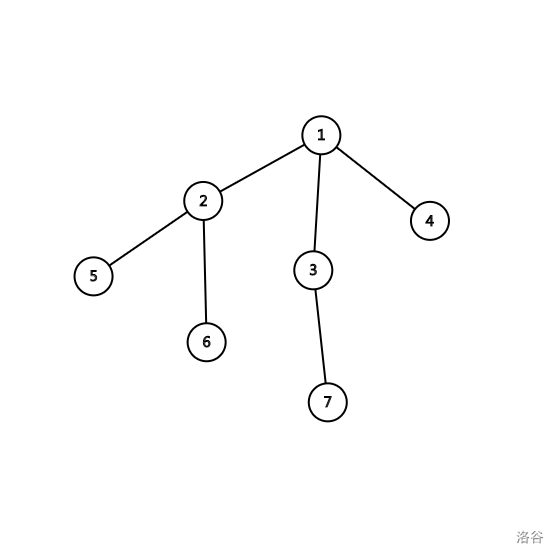
即用欧拉序+ R M Q +RMQ + R M Q O ( 1 ) O(1) O ( 1 ) L C A LCA L C A d f s dfs d f s d f s dfs d f s S T ST S T L C A LCA L C A R M Q RMQ R M Q
(1)预处理 1 2 3 4 5 6 7 8 9 10 11 void dfs (int u, int fa) dfn[u]=++tot; f[tot][0 ]=u; dep[u]=dep[fa]+1 ; for (int i=head[u];i;i=nxt[i]){ int v=vv[i]; if (v==fa) continue ; dfs (v, u); f[++tot][0 ]=u; } }
1 2 3 4 5 6 7 8 for (int i=1 ;i<20 ;++i) for (int j=1 ;j+(1 <<i)-1 <=tot;++j) if (dep[f[j][i-1 ]]<dep[f[j+(1 <<(i-1 ))][i-1 ]]) f[j][i]=f[j][i-1 ]; else f[j][i]=f[j+(1 <<(i-1 ))][i-1 ]; for (int i=2 ;i<=tot;++i) lg2[i]=lg2[i>>1 ]+1 ;
(2)查询 1 2 3 4 5 6 7 8 int lca (int a, int b) int l=dfn[a],r=dfn[b]; if (l>r) swap (l,r); int lg=lg2[r-l+1 ]; if (dep[f[l][lg]]<dep[f[r-(1 <<lg)+1 ][lg]]) return f[l][lg]; else return f[r-(1 <<lg)+1 ][lg]; }
3.求路径上最值 求树上两点a , b a,b a , b
我们再设一个g [ i ] [ j ] g[i][j] g [ i ] [ j ] i i i 2 j 2^j 2 j
g [ i ] [ j ] = m i n ( g [ i ] [ j − 1 ] , g [ f [ i ] [ j − 1 ] ] [ j − 1 ] ) g[i][j]=min(g[i][j−1],g[f[i][j−1]][j−1]) g [ i ] [ j ] = m i n ( g [ i ] [ j − 1 ] , g [ f [ i ] [ j − 1 ] ] [ j − 1 ] )